Question: What’s the difference between a normal 2D movie and a 3D movie?
Answer: In a 2D movie, each eye sees the same image. In a 3D movie, special glasses are used to ensure that each eye sees only the image that it is meant to see, and those two images were captured by two different cameras in slightly different locations.
3D movies work because they rely on your brain to reconstruct the 3D world using a pair of 2D images — something your brain does all the time, anyway. Try closing one eye and pressing the letter Y on the keyboard in front of you. Now do it again with both eyes open. Was it easier the second time? Repeat with other objects around you if you want.
You could say that photogrammetry is to human vision what aeronautical engineering is to bird flight.
So, the underlying concept of photogrammetry is more familiar to us that you might have imaged. But, in the same way that aeronautical engineering is a science with laws and equations that birds are completely oblivious to, photogrammetry as a science involves concepts and formulas that we can happily ignore while eating our popcorn in the cinema. But we can get an appreciation of the underlying principles without too much effort.
To begin with, I’m going to simplify the image capturing device (whether it’s a camera or the human eye) down to its essential components:
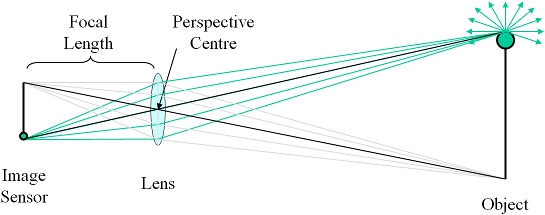
First, there is an image sensor, which would be the retina in a human eye, a frame of film in a film camera, or either a CCD or CMOS array in a digital camera. The image sensor is responsible for capturing the image that is projected onto it.
Secondly, there is a lens. The purpose of the lens is to ensure that all the light travelling from a single point in the real world that happens to hit the lens gets focussed on to the same point on the image sensor. (Note that the lens will only actually realise this goal for points in the real world that are at the focus distance; points nearer or farther away will end up with their light spread over a disc, the size of which depends on how far away they are from the focus distance, with the result that they will look blurry in the image. I may do an article on the role of the aperture later that will explore this in more detail.)
In the diagram above you can see that there are many green rays of light emanating from the top of the object travelling in all different directions. A subset of those rays is captured by the lens, and all of those rays end up at the same point on the image sensor. (There are also grey rays of light emanating from the bottom of the object which the lens simultaneously focusses onto a different location on the image sensor.)
From the point of view of photogrammetry, we can actually ignore all of the rays of light that pass through the lens from a single point except one — the light that happens to pass through the perspective centre of the lens. (These are shown in black above.) The significance of this point is that any ray of light passing through it, from any direction, will continue travelling in a straight line.
Because of this, if we look at any point in the image and reverse the direction of the ray from that point, back through the perspective centre, into the scene, we can tell which direction the light came from that was responsible for that point in the image.
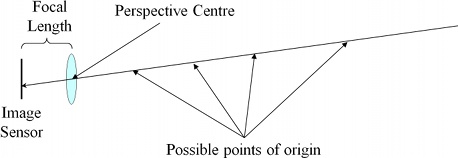
What we can’t tell is how far the light travelled before it hit our lens. It could have been millimetres, or it could have been ten billion light years. When we capture a 2D image of the 3D world, we lose depth information. We have no idea whether we’re looking at a big object far away, or a small object that’s much closer to us:
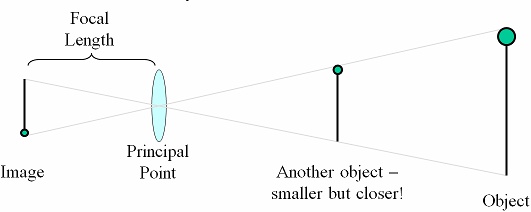
This was used to great effect in the movie Top Secret, where at the beginning of this particular scene we assume the phone appears to be large because it is really close to the camera, but when the guy picks it up we realise it is actually a really large phone:

With only a single image, our brain relies on other cues to determine 3D relationships (like knowing how big a phone should be), making jokes like this possible.
Of course, the joke wouldn’t work if the movie was in 3D. Why? Because we solve the problem of not knowing how far the light travelled before hitting the lens by taking another image from a different location and finding the same point in that image:
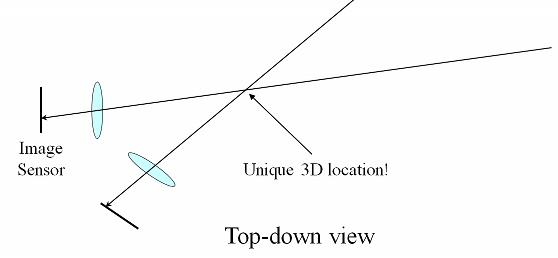
We now have two rays from the two different camera positions, and we can intersect those rays to find out where the light came from! If we saw that scene in 3D, then, we would know immediately how far away the phone was and, therefore, how big it actually was, which would spoil the surprise.
So, this is why you need two cameras to make a 3D movie, and why we need at least two camera positions to create 3D models of the real world with photogrammetry. (3D movies always use exactly two because we have two eyes and there’s nothing to see a third image with! Computers have no such limitations and so there is no requirement to limit ourselves to two images with photogrammetry, but we still obviously need at least two.)
For software to be able to reconstruct 3D models of the real world from those images, all it needs to be able to do is:
-
Figure out where the camera was and what direction it was pointing in when each image was captured. (We call these the exterior orientations of the images. One exterior orientation consists of six parameters — X, Y, and Z for the location of the camera, and ω, φ, and κ for the rotation of the camera.)
-
Recognise when it is looking at the same real-world locations when it is looking at the pixels in each image.
The following video from our YouTube channel shows this process in action:
When the user clicks on the “GO” button, the first thing the software does is determine the exterior orientation of each image. It does this by searching for and finding about 80 common points on the two images and then working out what the relationship must be between the camera positions in order for those 80 points to appear in the locations they appear within each image. (Before that the user digitised some control points — these are points in the images that have surveyed real-world co-ordinates. They aren’t required for this to work at all; they are simply an easy way of establishing a particular co-ordinate system for all the data to be in.)
Once it has done that, it pops up a dialog box to summarise the results and show how well the derived orientations matched the observations.
The video is recorded in real-time so you can see that the entire process takes about one second on a modern PC.
The next step is to identify common points in each image, intersect the rays formed by projecting those points back through the perspective centre using the exterior orientation to do so, and determining a 3D co-ordinate. (At the same time it also establishes the connectivity between points and uses that information to form triangles so that the user can map using a textured mesh rather than just a point cloud.)
That process takes anywhere from tens of seconds to several minutes, depending on the size of the images and the speed of the user’s PC. My computer can generate 10,000 points per second or more, including the time it takes to generate the triangular mesh.
Of course, this pales in comparison to the speed of the human brain, which processes the images captured by the eyes in realtime, but it’s still pretty impressive!
In an upcoming article I’ll look at what the limits of this approach are in terms of detail and accuracy, and how to calculate in advance what accuracy you should expect from a given setup. Stay tuned!
Pingback: Aerial Mapping with UAVs and 3DM Analyst Mine Mapping Suite « ADAM Technology Team Blog